LLL算法,即Lenstra-Lenstra-Lovász算法,是一种在多维向量空间中用于基底约减的多项式时间算法。它有助于解决数个与计算数学相关的问题,如求解整数线性方程、计算多项式的分解以及在密码学中破解满足某些条件的加密系统。在密码学中,LLL算法的重要性显而易见,因为它能够对加密算法如RSA进行有效的攻击,尤其是在主要参数...
背包问题通解: 当密度d满足以下条件时,LLL算法能有效地解决这类背包问题 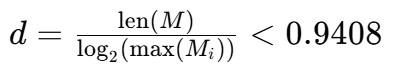 其中:
输入劣基,输出优基,LLL算法认为满足①Size条件和②Lovasz条件的基就比较优质了 格的维数n不太大时,LLL能把格的基变成优质的基(接近正交),利用优质的基容易求格的最短向量(SVP)等问题 做法: 输入:n个基向量{v1,v2,…vn} 令k=2,当k<=n时 循环以下三步 1.对n个基向量进行施密特正交化 ...
LLL算法简单来说就是: 将a lattice basis 转换为 LLL-reduced basis,去解决SVPγ问题,其中γ=2(n−1)/2。 “转换”就是要做Gram-Schmidt正交化,但要满足两个条件:1的意思就是系数有约束,必须都小于等于1/2。 两个基向量不要过小<=>Gram-Schmidt正交化不会太小 ...
LLL算法的具体流程如下: 输入:整数格基 第一步:计算正交基 第二步:约化步骤。如下: for i=2 to n for j=i-1 to 1 第三步:置换步骤。如下: 若存在 ,则置换 和 。 并返回到第一步; 输出: 备注:此算法中 符号代表取最接近的整数,例如
要深入理解LLL算法,可以从以下几个方面进行:一、明确算法基本概念 全称与提出者:LLL算法全称是LenstraLenstraLovász基整数近似算法,由Hendrik Lenstra父子和Laszlo Lovász于1982年提出。 算法目标:旨在解决在整数基下求解一个向量的最短向量问题。二、掌握核心逻辑 启发式规则:LLL算法的核心在于其启发...
1. LLL算法在计算机科学中有着广泛的应用,如计算机科学中的多项式近似、矩阵相乘等,并可被应用于许多不同的算法问题。 2. 算法基本思路是将给定的格分解为一个格基,然后找到一个新的格基,其基向量更短,并且更接近于原格。这个过程可以通过不断地将格分解为更小的子格并找到更短的基向量来实现。 3. LLL算法...
lll算法c语言 LL算法是一种语法分析算法,主要用于解析上下文无关文法。在C语言中,LL算法可以用来构建语法解析器,帮助程序员解析代码。本文将介绍LL算法的基本原理和C语言实现,以及如何使用LL算法构建一个简单的语法解析器。 LL算法中,LL代表Left-to-right, Leftmost derivation。这意味着算法从左到右扫描输入的字符,...
技术标签: SPFA LLL优化 SLF优化 双向队列优化 优化一. spfa的SLF优化,就是双向队列优化,在spfa压入队列时,判断要压入队首还是队尾。这个优化可以优化15%~20%。二. spfa的LLL优化,就是记录现在队列中元素所代表值的平均值,和要压入元素的值相比较,如果大于平均值,直接压入对列尾部,LLL优化+SLF优化可以优化...